各种排序算法解析和源码
选择排序
将一个序列中最小的元素同未排序序列的第一个进行交换
1 | package selectSort; |
插入排序
如果当前遍历的元素比已完成排序的序列的最后一个大,则遍历下一个,如果当前遍历的元素比已完成排序的序列的最后一个元素小,则遍历已经排序完的序列,将这个这个元素,插入到对应的位置
1 | package insertSort; |
希尔排序
根据步长将待排序的序列分为多个组,对每一个组进行排序,排完后将步长减小,继续进行分组排序,当步长变为一时,就是对整个序列进行排序,这样做最后一次查询的时候,序列中的数据已经基本有序了,此时再进行插入排序,就变得快多了
1 | package shellSort; |
冒泡排序
将数据两两比较,将大的往序列的后面进行交换(如果当前遍历的元素比后一个元素小则位置不变,继续向后遍历,如果当前遍历的元素比后一个元素大,则将当前元素同后一个元素进行交换)
1 | package bubbleSort; |
快速排序
选择一个基准数,每次将比基准数大的元素放到基准数的后面,将比基准数小的元素放到基准数的前面,这样整个序列就被分为了两半,然后再分别对这两半进行同样的操作,递归下去,直到这两半中都只有一个元素
1 | package quickSort; |
归并排序
将待排序的队列进行递归分解,分解为两部分,直到每个部分中都只有一个元素时,再将这两个部分进行归并,知道最后,将两半归并为一个序列
1 | package mergeSort; |
基数排序
将数字按照各个位的大小进行排序,并按先进先出的规则,这样排序的结果为:最高位按照顺序排序,最高位相同,按照次高位的顺序排序,一直到按照最低位排序
1 | package radixSort; |
堆排序
将序列构建为一个大顶堆或者小顶堆,然后将堆顶元素放到已排序序列的第一个,然后再将前面的元素进行重新构建,直到所有的元素都有序
1 | package heapSort; |
与数组初始状态无关的排序算法
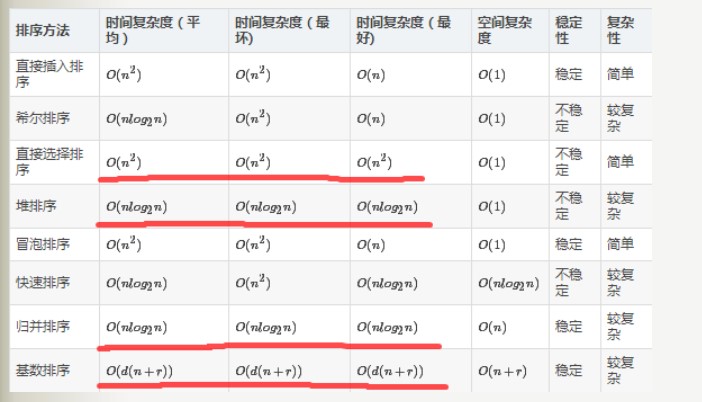
首先,与初始状态无关分为几种情况
- 算法复杂度与初始状态无关;
- 元素总比较次数与初始状态无关;
- 元素总移动次数与初始状态无关。
以下四种排序方法的算法复杂度与数组的初试状态无关:
一堆(堆排序)乌龟(归并排序)选(选择排序)基(基数排序)友
稍加判断得到,以上三种情况2、3是必定包含在情况1中间的。
- 堆排序
思想:首先对初始数组建立最小堆,然后取堆顶元素与堆尾交换,再此堆元素(不含堆尾)再重新构建最小堆,依次循环。
分析:由于建立最小堆其实就是将初始元素按照规定的准则进行一系列排序(包括层级向下比较、交换),所以如果元素一开始就已经是最小堆则不需要此时的交换且大大减少向下比较次数,
所以堆排序不属于情况二也不属于情况三。
- 归并排序
思想:将初试数组划分成N个子数组,两两进行合并排序,然后结果再和其他同级合并后的数组合并知道合并完所有。
分析:外层递归与初始无关,主要思考合并排序中的比较和交换即可。合并排序思想:将数组A第一个与数组B第一个比较,较小的那一个直接进入result数组并且指针向下移动再与对面数组第一个比较,依次类推,然后将还有剩余的数组内元素全放入result,最后用result将原数组中对应的值一一替换。因此,假设初始数组就是有序的,那么每次合并排序的时的比较次数都仅仅是一个待合并的数组的长度,因此比较次数与初始状态有关,归并排序不属于情况二。
然而,不论一开始的状态如何,最后都是两个数组进入result,移动次数都为两个待合并数组的长度和,然后再将result内元素全部移动到原来数组进行替换。所以元素移动次数与初始状态无关,归并排序属于情况三。
- 选择排序
思想:i 从头开始,每次遍历之后所有的元素,k 从 i 开始,向后标记最小的元素,循环后如果大于 i ,则与 i 位置元素交换,一直到最后。
分析:比较次数都是N-1的阶乘,与初始状态无关,所以选择排序属于情况二。
交换次数当全部已经排序好时则不发生交换,所以选择排序不属于情况三。
- 基数排序
思想:将数组从低位到高位,每到一位对应分入10个桶(0-9)中,依次到最高位,由于每上升一位,处于“0号桶”中的数据都会将此位之前的数字排好,以此达到排序效果。
分析:基数排序中并不发生任何元素之间的比较,所以基数排序属于情况二。
不论初始数组如何排列,都是从个位开始,各自进入自己个位对应的位置,之后也都是一样,所以元素移动次数一样,所以基数排序属于情况三。
综上所述:
1、算法复杂度与初始状态无关的有:选择排序、堆排序、归并排序、基数排序。
2、元素总比较次数与初始状态无关的有:选择排序、基数排序。
3、元素总移动次数与初始状态无关的有:归并排序、基数排序。


